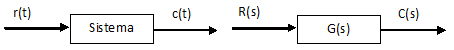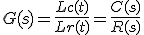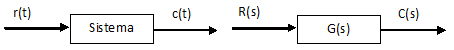 |
Imagen 14. Recurso propio.
|
Matemáticamente se representará:
Características de la función de transferencia (FDT):
La función de transferencia es una propiedad del sistema y depende de las propiedades físicas de los componentes del sistema, es por tanto independiente de las entradas aplicadas.
- La función de transferencia viene dada como el cociente de dos polinomios en la variable compleja s de Laplace, uno, N(s) (numerador) y otro D(s) (denominador).
- El grado del denominador de la función de transferencia es el orden del sistema.
- Distintos sistemas pueden compartir la misma función de transferencia, por lo que ésta no proporciona información a cerca de la estructura interna del mismo.
- Conocida la función de transferencia de un sistema se puede estudiar la salida del mismo para distintos tipos de entradas. La función de transferencia es muy útil para, una vez calculada la transformada de Laplace de la entrada, conocer de forma inmediata la transformada de Laplace de la salida. Calculando la trasformada inversa se obtiene la respuesta en el tiempo del sistema ante esa entrada determinada.
- El polinomio del denominador de la función de transferencia, D(s), se llama función característica, ya que determina, por medio de los valores de sus coeficientes, las características físicas de los elementos que componen el sistema, independientemente de la excitación que posea y perturbaciones que pudiera tener.
- La función característica igualada a cero (D(s)=0) se conoce como ecuación característica del sistema:
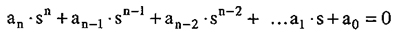
Las raíces de la ecuación característica se denominan
polos del sistema. Las raíces del numerador N(s) reciben el nombre de
ceros del sistema.